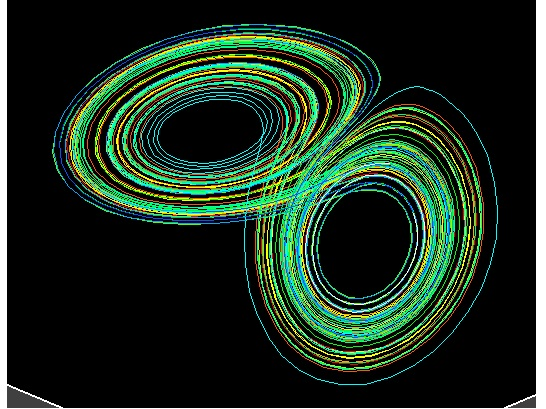混沌理論

混沌理論（chaos theory）它是一種定性思維和定量分析相結合的方法，用于探索動態系統（如：人口移動、化學反應、氣象變化、社會行為等）必須用整體的連續的而不是單一的數據關系來解釋和預測的行為。

1963年，美國氣象學家愛德華·諾頓·洛倫茨提出了混沌理論（Chaos）非線性系統的多樣性和多尺度性。混沌理論解釋了決策系統可能產生隨機結果。該理論的最大貢獻是用簡單的模型獲得清晰的非周期結果。在氣象、它在航空航天的研究中起著重要的作用。

混沌理論認為，在一個混沌系統中，初始條件發生非常微小的變化，經過不斷的放大，就會造成其未來狀態的巨大差異。我們可以用西方世界流傳的一首民歌來說明這個形象。這首民謠說：

釘子缺，蹄鐵卸；蹄鐵卸，戰馬蹶；戰馬蹶，騎士絕；騎士絕，戰事折；戰事折，國家滅。

馬蹄鐵上的釘子是否會丟失是初始條件的一個非常小的變化，但它“長期”效果是一個帝國生死存亡的根本區別。這就是軍事政治領域所謂的“蝴蝶效應”混沌系統對外界刺激的反應比非混沌系統快。

混沌現象是由于物體按照一定的規律不斷復制前一階段的運動狀態，產生不可預測的隨機效應。所謂“錯誤再小也是錯”是對這種現象最好的注解。具體來說，混沌發生在一個可變化的物體或系統中，在動作開始時非常簡單，但經過一定規則的連續變化，產生了意想不到的后果，即混沌狀態。但是，這種混沌狀態不同于一般的混沌狀態經過長期完整的分析，可以從這種混亂的現象中梳理出一些規律。雖然混沌最初是用來解釋自然的，但它在人文和社會領域尤其常見，因為事物之間是相互牽引的。比如股市的漲跌、人生的平坦曲折、教育的復雜過程。

1)隨機性：系統的混沌狀態是由系統內部動力學的隨機性引起的不規則行為，通常稱為內部隨機性．例如，在一維非線性映射中，即使描述系統演化行為的數學模型不包含任何附加的隨機項，即使控制參數、初始值都是確定的，但系統在混沌區的行為仍然是隨機的。這種隨機性是在系統中自發產生的，與外界的隨機性有著完全不同的來源和機制它顯然是確定性系統中的內在隨機性和機制函數。系統中的局部不穩定性是內部隨機性的特征，也是對初值敏感的原因。

2)敏感性：系統的混沌運動，無論離散還是連續，低維還是高維，保守還是耗散。無論是時間演化還是空間分布都有一個基本特征，就是系統的運動軌道對初始值極其敏感。這種敏感性，一方面反映了非線性動力系統中隨機系統的運動趨勢的強烈影響；另一方面，也會導致系統長期行為的不可預測性。氣象學家洛倫茨提出了所謂的'蝴蝶效應'是對這種敏感性的突出而生動的解釋。

3)分維性：混沌具有分形維數的性質，這意味著相空間中系統運動軌道的幾何形狀可以用分形維數來描述。比如科赫雪花曲線的分形維數是1.26；描述大氣混沌的洛倫茲模型的分形維數為2.06系統的混沌運動在相空間中無限糾纏、折疊和扭結形成了具有無限層次的自相似結構。

4)普適性：當系統趨于混沌時，特征具有普遍意義。其特性不隨具體系統和系統運動方程的不同而改變。所有這些系統都與費根鮑姆常數有關。

5)標度律：混沌是一種無周期性的有序狀態，具有無限的自相似結構和無標度區。只要數值計算的精度或者實驗的分辨率足夠高，就可以發現小尺度混沌的有序運動模式，所以它具有標度律的性質。比如在倍周期分岔過程中，混沌吸引子的無限嵌套相似結構，從層次關系上看，具有結構的自相似性和尺度變換下的結構不變性，從而表現出有序性。

混沌理論的另一個特點是它的發展，它有三個原理：

1、能量總是沿著阻力最小的路徑前進

2、總有一個看不見的基本結構，決定了阻力最小的路徑。

3、這種無時無刻不在通常看不見的基本結構不僅可以被發現，而且可以被改變。

混沌理論

混沌理論是一種定性思維和定量分析的方法，用于討論動態 系統的行為不能用單一的數據關系來解釋和預測，而是用一個整體的連續的數據關系來解釋和預測。

一切事物的原始狀態都是一堆看似不相關的碎片，但這種混亂狀態結束后，這些無機的碎片就會有機地整合成一個整體”

混沌一詞原本是指宇宙形成前的混沌狀態古希臘哲學家持宇宙始于混沌論，認為宇宙是從混沌開始逐漸形成有序世界的。在有序的宇宙中，西方自然科學家經過長時間的討論，逐一發現了自然界中的許多規律，如萬有引力杠桿原理相對論等等。這些自然規律可以用一個單一的數學公式來描述，根據這個公式可以準確地預測物體的行為。

在過去的半個世紀里，科學家發現許多自然現象可以簡化為簡單的數學公式，但它們的行為是無法預測的。例如，氣象學家Edward Lorenz發現，簡單的熱對流實際上可以引起難以想象的氣象變化，從而導致所謂的“蝴蝶效應”20世紀60年代，美國數學家Stephen Smale發現，某些物體的行為發生某種規律性的變化后，后續的發展沒有一定的軌跡可循，呈現出一種無序的混沌狀態。

社會方面

混沌理論，尤其是蝴蝶效應，通常用于天氣、在一個很難預測某一段時間的復雜系統中，比如股票市場。如果差距越來越大，破壞性會很大。為什么天氣或股市會出現崩盤和不可預測的自然災害。

社會學中用蝴蝶效應來說明：一個微小的機制，如果不及時引導、監管可能給社會帶來巨大危害，被戲稱為“龍卷風”或“風暴”一個微小的機制，只要引導正確，經過一段時間的努力，很可能會產生轟動效應，或者說“革命”

經濟方面

2003年，美國發現一例疑似瘋牛病病例，隨即給剛剛復蘇的美國經濟帶來毀滅性颶風。扇動“蝴蝶翅膀”是的，它 那個不幸的人是誰“瘋牛”首先，總產值1750億美元140萬個就業崗位的美國牛肉產業受到沖擊；作為牛主主要飼料來源的美國玉米和大豆產業也受到影響，其期貨價格呈下跌趨勢。但最終，它會火上澆油“瘋牛病颶風”最大的損失是美國消費者的減少對牛肉制品的信心。

1998年亞洲金融危機，美國股市風暴，其實都是經濟運行混沌理論中的現象；ソースなし販売モデル 今は電子商取引の最も科學的なモデルです このモデルは一人一人の経営に適している だから。：輸入端的微小差異會迅速放大到輸出端的巨大差異。看起來，今天北京的一只蝴蝶扇動翅膀，可能會引發大氣中的一系列事件，可能會導致一個月后紐約的一場風暴。

語言方面

混沌理論被廣泛應用于語言研究領域。學術界用蝴蝶效應來解釋和研究混沌語言現象比如《人民日報》在2010年11月10日頭版發表了一篇題為《江蘇給力“文化強省”》的文章由于其權威性和號召力，一直被限制在網絡使用“給力”這個詞一夜之間在中國流行起來，蔓延到國家詞匯系統，被收入第六版《現代漢語詞典》。

20世紀80年代，學術界開始用混沌理論及其蝴蝶效應研究語言問題。1991年在美國伯克利舉行“語言研究的新方法和新視野”在研討會上，中國數學家、語言學家周海中教授曾建議建立“語言混沌論”他指出，語言混沌理論主要從混沌理論的角度考察語言及其相關現象，用混沌理論解決語言及其相關現象的非線性問題；為了促進混沌語言研究的發展，有必要建立一種新的語言研究范式。就目前情況來看，這種新的語言研究范式正在興起。

混沌的發現揭示了我們對法律和由此產生的行為之間的關系的理解－也就是因果之間－對關系的基本誤解。我們曾經認為簡單的原因必然產生簡單的結果(這意味著復雜的結果必然有復雜的原因)但是現在我們知道簡單的原因可以產生復雜的結果。我們意識到知道這些規律并不意味著我們可以預測未來的行為。

這個想法已經被一群數學家和物理學家采納，包括威廉·迪托 (William   ditto)艾倫·加芬科(Alan   garfinkel)和吉姆·約克 (Jim   York)，已經成為非常有用的實用技術，他們稱之為混沌控制。本質上，這個想法是讓蝴蝶效應為你所用。初始條件的小變化會導致后續行為的大變化，這可能是一個優勢；你所要做的就是確保你得到你想要的大改變。了解混沌動力學是如何工作的，使我們有可能設計出一種可以完全實現這一要求的控制方案。

這種方法已經取得了一些成功。混沌控制最早的成就之一就是只用衛星上剩下的很少量的聯氨來制造一個“死”衛星改變了軌道，與一顆小行星相撞。美國國家航空航天局NASA操縱衛星繞月球旋轉五次，每次 都用一點聯氨輕推衛星，最后相撞。

混沌理論的特征也存在于證券市場中。周k線圖看起來像日k線圖、小時K線圖、5分鐘k線圖的形態非常相似，這是股票市場價格的分形特征我們可以用5分鐘k線圖或者小時k線圖來推斷日k線圖或者周k線圖的形態，為投資決策服務。

在過去的半個世紀里，科學家發現許多自然現象可以簡化為簡單的數學公式，但它們的行為是無法預測的。例如，氣象學家Edward Lorenz發現，簡單的熱對流實際上可以引起難以想象的氣象變化，從而導致所謂的“蝴蝶效應”也就是幾個月前發現的某次地下大雪，是蝴蝶在異地扇動翅膀產生的氣流造成的。

20世紀60年代，美國數學家Stephen Smale 發現，經過一些規律性的變化后，一些物體的后續發展并沒有一定的軌跡，呈現出混沌狀態。

混沌控制由狄透（William   ditto）賈芬卡（Alan   garfinkel）約克（Jim   York）把這個想法變成實用的技術，從小的變化開始，引起希望和思維的大變化。